My Year 10 have recently been working with Pythagoras in 3-D objects, and quite typically in my experience they were having difficulty identifying suitable triangles to calculate some of the lengths; particularly those lengths that go through a shape requiring multiple applications of Pythagoras. Being ready for this I decided to try an approach that I had been considering that links the number of applications of Pythagoras' Theorem to the number of dimensions that the line moves through. The approach met with some success and I can see how it might have real potential in linking to dimensional analysis so I thought I would outline it here.
The first and one of the key points was to ensure that pupils understood that Pythagoras' Theorem is a relationship concerning area. Although we often use Pythagoras' Theorem to solve for missing lengths, the actual essence of the relationship is between the areas of three squares where two of them meet to form a right angle. The image below is one that is typically used to illustrate this (and one I have used lots in the past).
The first and one of the key points was to ensure that pupils understood that Pythagoras' Theorem is a relationship concerning area. Although we often use Pythagoras' Theorem to solve for missing lengths, the actual essence of the relationship is between the areas of three squares where two of them meet to form a right angle. The image below is one that is typically used to illustrate this (and one I have used lots in the past).
Once my pupils understand that this is a relationship area, the discussion is then turned to dimensions. What I am hoping to show pupils is that the two shorter sides of a right triangle are lines that only move in one dimension, whereas the diagonal moves in two (as the two sides are at right angles they can be considered to be two independent dimensions). So Pythagoras' Theorem can be thought of as a relationship that starts with lines moving in a single dimension, and relates them to a line moving in two dimensions (linking to area being a two dimensional concept).
Now let us consider a cuboid like the one below:
An early job of work to do with pupils here is to make sure they can identify lines that move in one, two or three dimensions. Generally for me this leads to lots of gesturing around the room and drawing imaginary lines along walls and floors, as well as between corners across the room. Once pupils understand how these lines are moving we can start looking at which distance can be solved with only one application of Pythagoras' Theorem and which cannot. For example in the cuboid above the distances AF, BD, FC etc can all be solved directly using a single application of Pythagoras' Theorem as they are all lines that move in two dimension.
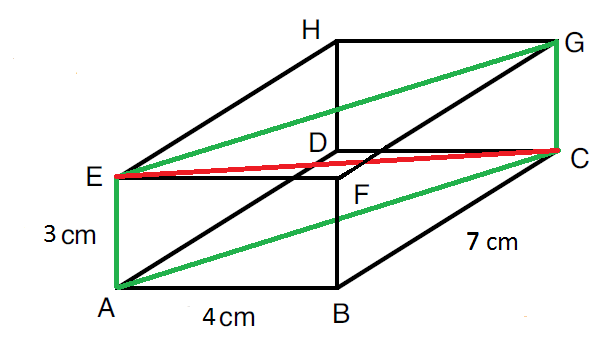
Now let us consider a line that moves in three dimensions, for example EC. A tip from me on this, before drawing the triangle in the shape, try drawing the rectangle first (as below). For some reason pupils see this more easily that just the triangle.
The discussion we had here is that we cannot expect to solve for lengths like this with one application of Pythagoras, because this length moves in all three dimensions and Pythagoras' Theorem is a two dimensional relationship. In order to solve this problem we are going to need two applications of Pythagoras, one to relate two of the one-dimensional lines with a line that moves in two dimensions (in the above case either EG or AC will do the job) and then to use this line moving in two dimensions with the line moving in the third dimension to relate to the line moving in all three dimensions.
To some this might seem like overkill, but what it does is give pupils an objective test as to whether a line can be solved using given information - if it moves in more than two dimensions it cannot be solved by a single application of Pythagoras' Theorem using lines that only move in one dimension. Of course from here you can complicate things and look at other three dimensional shapes, begin to make judgements about whether line can be considered to move in only one dimension (right-angled to each other), two dimensions or three dimensions. I also think it reinforces area as a key concept and will provide a nice link to dimensional analysis of different formulae when it comes to looking at that concept in more depth.
So in the future I think I will definitely be talking about Pythagoras' Theorem as an area relationship, and definitely be talking about dimensions that lines move in more formally with pupils; if your pupils are having trouble applying Pythagoras' Theorem to three dimensions why not try it as well?


No comments:
Post a Comment